P1034 矩形框遮盖 题型叙述

在平面图上带n个点（n<=50），每一点用一对整数金额座标表达。比如：当n＝4时，4个点的座标分另为：p1（1，1），p2（2，2），p3（3，6），P4（0，7），见图一。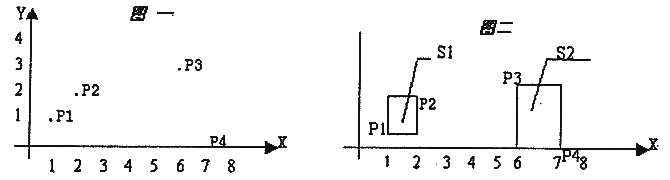

这种点能够 用 k 个矩形框（1<=k<=4）所有遮盖，矩形框的边平行面于纵坐标。当 k=2 时，能用如图所示二的2个矩形框 sl，s2 遮盖，s1，s2 总面积和为 4。难题是当 n 个点座标和 k 得出后，怎么才能促使遮盖全部点的 k 个矩形框的总面积总和为最少呢。承诺：遮盖一个点的矩形框总面积为 0；遮盖平行面于纵坐标平行线上面的矩形框总面积也为0。每个矩形框务必彻底分离（边框线与端点也都不可以重叠）。

键入文件格式

n k
xl y1
x2 y2
… …
xn yn
(0<=xi,yi<=500)

輸出文件格式

輸出至显示屏。文件格式为：
一个整数金额，即符合条件的最少的矩形框总面积总和。

I/O示例 键入

4 2
1 1
2 2
3 6
0 7

輸出

4

剖析

关键是检索。
这题修枝方式好像各种各样。
下边即将展现编码的作法：
将读入的座标按x和y由小到大排列，随后检索将持续的i个点分别在一起，期内分辨难题是不是行得通，及其开展各种各样小提升。
Code

#include#include#include#include#includeusing namespace std;
int read(){
    int x=0,f=1;char ch=getchar();
    while(ch'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
struct point{
    int x,y;
}a[60];
int cmp(point a,point b){
    if(a.x==b.x)return a.y<b.y;
    return a.xn){
        ans=min(ans,smm);
        return;
    }
    if(cnt>k)return;
    int i,j;
    b[cnt].x1=a[pos].x;
    b[cnt].x2=a[pos].x;
    b[cnt].y1=a[pos].y;
    b[cnt].y2=a[pos].y;
    for(i=pos;i<=n;i++){
        b[cnt].y2=max(b[cnt].y2,a[i].y);
        b[cnt].x2=max(b[cnt].x2,a[i].x);
        b[cnt].x1=min(b[cnt].x1,a[i].x);
        b[cnt].y1=min(b[cnt].y1,a[i].y);
        for(j=1;j<cnt;j++){
            if(b[cnt].x1<=b[j].x2 && b[cnt].y1<=b[j].y2)return;
        }
        if(i<n && cnt==k)continue;
        DFS(i+1,cnt+1,smm+(b[cnt].x2-b[cnt].x1)*(b[cnt].y2-b[cnt].y1));
    }
    return;
}
int main(){
    n=read();k=read();
    int i,j;
    for(i=1;i<=n;i++){
        a[i].y=read();a[i].x=read();
    }
    sort(a+1,a+n+1,cmp);
    memset(b,-1,sizeof b);
    DFS(1,1,0);
    printf("%d\n",ans);
    return 0;
}